A CARA APASIONANTE E MÁXICA DAS “MATES”.

Quen, nalgunha ocasión, non se ten feito preguntas como ¿ para que serven as matemáticas? ou ¿ ten algunha utilidade todo ese tempo adicado a resolver difíciles exercicios?.

Pois ben, as matemáticas son importantes en moitas disciplinas como a física, a enxenería ou a xestión empresarial e tamén forman parte da nosa vida diaria máis do que pensamos. Pero tamén existe un lado divertido e estimulante das matemáticas.

¿ Quen non se “ enganchou” algunha vez a un enigma ou a un xogo matemático e non parou ata resolvelo?. Enfrentarnos a un enigma mantén a nosa mente en alerta, estimula a imaxinación e desarrolla e axiliza a facultade de razoamento.

A continuación preséntase, según a temática dos problemas, os distintos bloques:

- ENIGMAS como actividade lúdica e de comprensión de enunciados.

- PROBLEMAS DE XEOMETRÍA , donde intervén solución plástica.

- LÓXICA, con problemas de razoamento nos que hai que facer uso da

coherencia.

- PROBLEMAS CLÁSICOS, eses nos que todos nos rompimos a cabeza para atopar as curiosas e orixinais solucións.

ENIGMAS

1.- AS BOMBILLAS E OS INTERRUPTORES.

Na primeira planta dunha vivenda temos tres bombillas e na planta baixa tres interruptores. Cada un dos interruptores encende unha bombilla . ¿ Como podemos saber , subindo soamente unha vez ó primeiro piso, que interruptor encende cada bombilla?.

2.- AS TRES BOLSAS DE CARAMELOS.

Teño 48 caramelos en 3 bolsas. Se da primeira bolsa paso á segunda tantos caramelos como hai na terceira, despois paso da segunda bolsa 6 caramelos á primeirae, para rematar, paso á terceira bolsa 4 caramelos da segunda . O resultado é que teño agora a mesma cantidade de caramelos nas 3bolsas. ¿ Cantos caramelos tiña inicialmente en cada unha das bolsas?.

3.- A PONTE E MARÍA.

María ten que pasar unha ponte que só soporta un peso máximo de 80 Kg. María pesa e leva con ela un bolso que pesa 8 Kg. María, por se acaso, colle o seu bolso e tírao ó outro lado da onte. Despois, xa tranquila, disponse a pasar a ponte, pero no momento en que a pisa, esta despréndese. ¿ Como é posible?.

4.- OS FILLOS DE ROSANA.

Eu teño seis fillos . Cada fillo ten unha irmá. ¿ Cantos fillos teño?.

5.- NEGRO MOI NEGRO.

Un coche de color negro coas luces apagadas circula por unha rua que non ten farolas e donde ningunha casa ten as luces encendidas. De repente crúzaselle un gato negro. Aínda así o conductor pode esquivalo. ¿ Como podes explicalo?.

6.- A TORMENTA DE ESCAIRÓN.

Hai uns anos, en Escairón houbo unha gran tormenta a media noite. ¿ É posible que 72 horas despois fixese un tempo soleado?.

7.- O GALIMATÍAS DA IRMÁ QUE NON É TÍA.

Eu teño unha tía e a miña tía unha irmá que non é tía miña. ¿ Como é posible?.

8.- UNHA IDADE MOI EXTRAÑA.

ANTONTE TIÑA 12 ANOS E O ANO QUE VEN FAREI 15. ¿ É POSIBLE ESTA CIRCUNSTANCIA?

9.- OS CORTES DE MARISA.

MARISA CORTA CADA MINUTO UN METRO DUNHA TEA QUE MIDE DEZ METROS. ¿CANTO TARDARÁ EN TE-LA COMPLETAMENTE CORTADA?

10.- UNHA PREGUNTA SOBRE A SELVA.

¿ATA QUE PUNTO PODE UNHA PERSOA ENTRAR NA SELVA?

11.- UNHA CONFESIÓN INEXPLICABLE.

DI FERNANDO: “A PERSOA QUE MÁIS QUERO NESTE MUNDO É, PRECISAMENTE, A SOGRA DA MULLER DO MEU IRMÁN”. ¿SABES QUEN É ESA PERSOA?

12.-O ENIGMA DOS IRMÁNS E IRMÁS.

XULIÁN TEN TANTOS IRMÁNS COMA IRMÁS; SEN EMBARGO, A SÚA IRMÁ LORENA TEN O DOBRE DE IRMÁNS QUE DE IRMÁS. ¿CANTOS HOMES E MULLERES HAI NA FAMILIA ?

13 .- O RELOXO DE PAREDE.

UN RELOXO DE PAREDE TARDA 5 SEGUNDOS EN DAR AS SEIS. ¿CANTO TARDARÁ EN DAR AS DOCE?.

14.- UN XOGO DE DADOS.

¿CAL É A SUMA DE PUNTOS MÁXIMA QUE SE PODE OBTER TIRANDO SIMULTÁNEAMENTE CATRO DADOS, TENDO EN CONTA QUE NINGÚN NÚMERO PODE REPETIRSE?.

15.- O CAMIÑO DE PENAVELLA.

INDO EU PARA PENAVELLA CRUCEIME CON 7 VELLAS. CADA VELLA LEVABA 7 SACOS. CADA SACO, 7 OVELLAS. ¿CANTAS VELLAS E OVELLAS IAN PARA PENAVELLA?.

PROBLEMAS CLÁSICOS.

1.-A CADEA BRANCA.

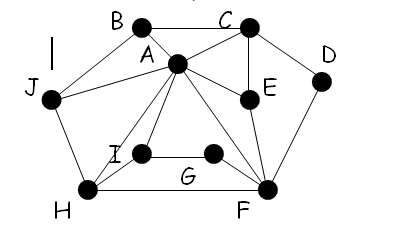
UNHA CADEA DE ESTABLECEMENTOS DE ELECTRODOMÉSTICOS TEN A CENTRAL EN A, E SUCURSAIS NAS CIDADES B,C,D,E,F,G,H,I,J. O SUPERVISOR, QUE TEN A SÚA OFICINA NA CIDADE A, QUERE FACER UNHA VISITA DE INSPECCIÓN A TÓDALAS SUCURSAIS. NON QUERE PASAR DÚAS VECES POLA MESMA CIDADE NIN POLO MESMO CAMIÑO. ¿EN QUE ORDE ORGANIZARÁ A VISITA?.

2.- O PROBLEMA DOS CUBOS.

¿QUE NÚMEROS MENORES DE 50 SE PODEN EXPRESAR COMO SUMA DE DOUS CUBOS?. POR EXEMPLO: 35=23 + 33

3.- .- O PLANO DO MUSEO.

ESTE É O PLANO DE ESPACIOS DUN MUSEO. ¿DE CANTAS MANEIRAS DIFERENTES SE PODE PERCORRER DESDE A ENTRADA ATA A SAÍDA, SEN PASAR DÚAS VECES POLO MESMO ESPACIO?

ENTRADA

1	2	3
4	5	6
7	8	9

SAÍDA

4.- .- DATAS CURIOSAS.

O 19 DE SETEMBRO DE 1991 É UNHA DATA CAPICÚA. ¿CAL SERÁ A SEGUINTE DATA CAPICÚA?.

5.- NÚMEROS E CASILLAS.

OBSERVA ESTE RECTÁNGULO DE CINCO CASILLAS.

2 3 5 8 13

NAS DÚAS PRIMEIRAS CASILLAS ESTÁN OS NÚMEROS 2 E 3 . SE SUMAS DOUS E TRES RESULTA CINCO, QUE É O TERCEIRO NÚMERO, E ASÍ SUCESIVAMENTE. COMPLETA SEGUINDO ESTA REGRA, O RECTÁNGULO SEGUINTE:

5 16

6.- .- INVESTIGAMOS NÚMEROS.

¿QUÉ TRES CIFRAS POÑERÍAS NAS CASILLAS DA PARTE SUPERIOR PARA QUE CUMPRAN TÓDALAS CONDICIÓNS QUE CHE SE INDICAN?.

1	2	3	NON HAI NINGUNHA CIFRA COMÚN
4	5	6	HAI UNHA CIFRA COMÚN
6	1	2	HAI UNHA CIFRA COMÚN, PERO MAL COLOCADA
5	4	7	HAI UNHA CIFRA COMÚN, PERO MAL COLOCADA
8	4	3	HAI UNHA CIFRA COMÚN E NO SEU SITIO

LÓXICA

1.- .- ESCRIBINDO O NÚMERO 1.000.

¿COMO SE PODE ESCRIBIR O NÚMERO 1.000 UTILIZANDO CINCO VECES O NÚMERO 9?

2.- .- A NAI E A FILLA.

UNHA NAI E A SÚA FILLA TEÑEN EN CONXUNTO 55 ANOS; A SÚA IDADE RESPECTIVA ESTÁ COMPOSTA POLAS DÚAS MESMAS CIFRAS PERO COLOCADAS Ó REVÉS. ¿CAL É A IDADE DE CADA UNHA?.

XEOMETRÍA

1.- .- O CÁLCULO DO ÁNGULO.

NO TRIÁNGULO ISÓSCELES, O ÁNGULO a MIDE 50º.¿ CAL É A MEDIDA DO ÁNGULO d ?

2.- O TERREO DA SEÑORA CAROLINA.

A SEÑORA CAROLINA TEN UNHA LEIRA TRAPEZOIDAL. QUERE REPARTILA ENTRE OS SEUS CATRO FILLOS. A CADA FILLO QUERELLE DAR UN ANACO IDÉNTICO DE TERREO. AXÚDALLE A FACELO.

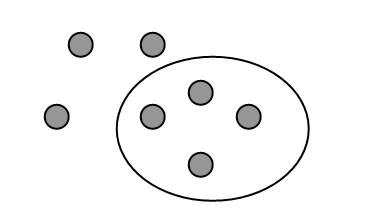
3.- AS FICHAS DE MARÍA.

MARÍA COLOCA SOBRE A MESA 7 FICHAS E DIBUXA UN CÍRCULO ARREDOR DE CATRO FICHAS. DIBUXADE VOS DOUS CÍRCULOS MÁIS RODEANDO CATRO FICHAS DE MANEIRA QUE CADA FICHA QUEDE SEPARADA DAS OUTRAS.