
Bingo aritmético
Presentación
Propoñémonos identificar clara e minuciosamente que procesos (xerais de pensamento e específicos das respectivas disciplinas, no noso caso, da matemática) se relacionan cos contidos de aprendizaxe que os currículos oficiais establecen e coas metodoloxías didácticas que os soportan e, segundo avanzamos niso, deseñar actividades realizables nas aulas que, a través do traballo docente, promovan expresamente o desenvolvemento dos ditos procesos, contribuíndo así ao logro de competencias.
Principios pedagóxicos
Entre os obxectivos educativos enunciados pola Unión Europea no Consello Europeo de Lisboa do ano 2000, ratificados ese mesmo ano no Memorando de Bruxelas sobre a aprendizaxe, para este traballo centrámonos naqueles que se refiren a:
i) Unha educación de alta calidade para todos, que xere actitudes positivas cara a aprendizaxe e capacite para “aprender a aprender”.
ii) Integrar correctamente as perspectivas culturais e as experiencias vitais dos alumnos, tanto nos contidos coma nos métodos.
iii) Focalizar as aptitudes básicas arredor da cultura tecnolóxica, ao espírito emprendedor e ás habilidades de socialización. O cometido do ensino será o de nutrir esa capacidade do ser humano para crear e usar coñecementos.
En coherencia co anterior, presentamos actividades que:
i) Integren as experiencias do alumnado.
ii) Conteñan propostas dinámicas que propugnen a interacción coa contorna.
iii) Planifiquen tarefas cunha metodoloxía interdisciplinar e/ou globalizada.
iv) Recreen os contidos a partir de centros de interese do alumnado, garantindo que sexan significativos para el.
v) Afiancen o desenvolvemento persoal e a autoestima.
vi) Potencien a adquisición de habilidades culturais e científicas básicas, acordes co nivel ao que correspondan.
vii) Susciten o emprego das novas tecnoloxías.
viii) Establezan medidas que contribúan ao tratamento da diversidade.
ix) Contribúan a desenvolver hábitos de estudo e traballo, individual e en equipo.
Eixes metodolóxicos
Na competencia matemática, alén doutras, inclúense habilidades para utilizar e relacionar números e capacidades para producir e interpretar mensaxes de contido cuantitativo.
Pola súa banda, na competencia en comunicación lingüística trátase de afondar máis alá do que estritamente requiren a recepción e a transmisión de información, para involucrarse na organización e na estruturación do propio pensamento.
E xa na competencia no coñecemento e na interacción co mundo físico, sinalamos a percepción do que nos rodea, tanto na contorna inmediata coma a grande escala, e a habilidade para comprender e resolver problemas nos que interveñan os obxectos observados.
Deséñanse actividades de aula que cohesionen os ámbitos sinalados, de maneira que as prácticas matemáticas involucren exercicios lingüísticos e, asemade, recreacións da contorna –desde o máis próximo ata o máis universal–.
En esencia, trátase dunha mesma estratexia didáctico-pedagóxica que se desenvolve para se adaptar aos diferentes ciclos, e aínda cursos, de primaria:
Fomentar o cálculo mental como aprendizaxe aritmética e como ximnasia da mente. Así, nenos e nenas terán que elixir números entre os dispoñibles e procurar combinacións deles que lles permitan obter como resultados outros números desexados. Isto supón un cambio de paradigma respecto da instrución estándar en matemáticas, na que se trataba de encontrar un resultado preestablecido a partir duns datos específicos.
i) Construír por escrito un enunciado dun problema relativo a unha situación significativa –real ou imaxinaria–, na que datos, resultado e proceso de solución se correspondan co que mentalmente acabarían de realizar.
ii) Variar os escenarios nos que acontecerán os problemas, de xeito que se realice un percorrido desde o inmediato ata o xeral.
A presentación por medio dun xogo estimulará a participación activa do alumnado. A versatilidade é total, de maneira que podemos adaptar a conveniencia números, operacións e imaxes que definen os contextos.
Exemplo de primeiro ciclo
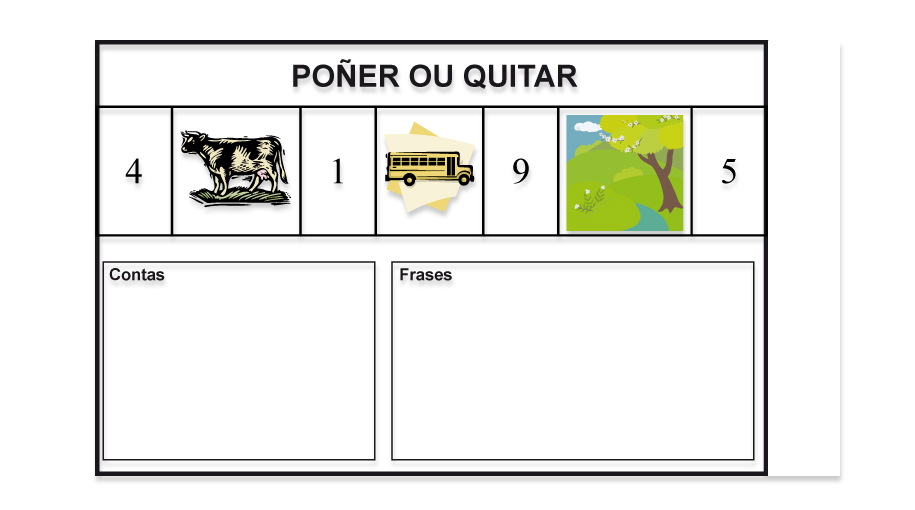
Trátase de completar o cartón sen necesidade de esperar polos catro números. Por exemplo, se saíron o 4 e o 5, o neno ou nena pode facer as contas:
4 + 5 = 9, conseguido! e 5 - 4 = 1, conseguido e completado!
Daquela, ten que buscar combinacións dos números que saísen do seu cartón que dean lugar a outros números do propio cartón. Os cartóns deséñanse para o abano numérico que se considere, de maneira que as posibilidades sexan múltiples, como no exemplo:
Nótese que tamén,
co 4 e o 1 obteriamos o 5 (4 + 1 = 5)
co 4 e o 9 podemos obter o 5 (9 – 4 = 5),
co 1 e o 5 obtemos o 4 (5 – 1 = 4)
co 9 e o 5 podemos obter o 4 (9 – 5 = 4).
Cada resultado conseguido esixe construír unha frase onde o realizado se aplique nas cousas representadas nos debuxos, ou sexa, enunciar un problema. Por exemplo, para a conta 4 + 5 = 9 podería ser:
Había 4 vacas no monte, o camión trouxo 5 e agora hai 9.
Versatilidade de escenarios: vemos outro exemplo para ilustrala. Debemos ter en conta que os cartóns se distribúen aleatoriamente e que é un xogo académico susceptible de realizarse con frecuencia, co cal o impacto matemático, lingüístico e físico-social será o desexado.
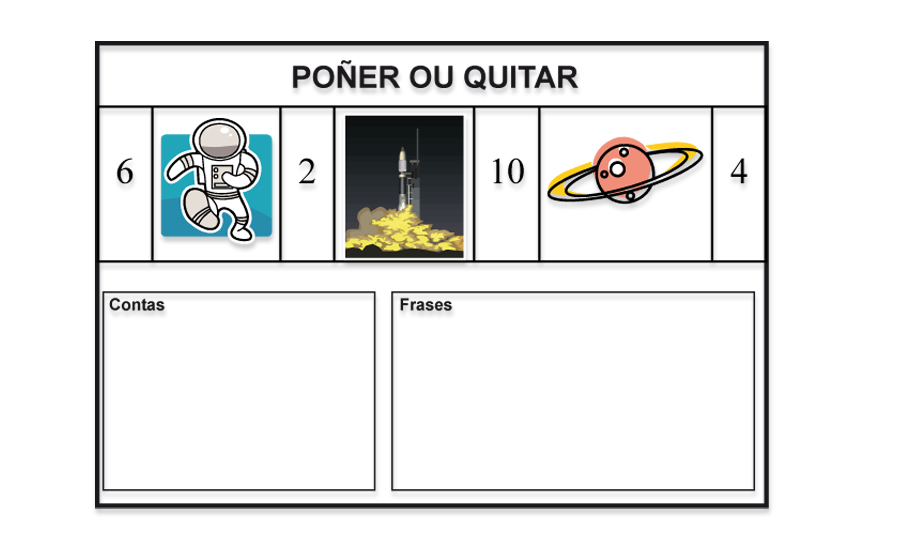
Orientacións para o tratamento da diversidade
É obvio que a dificultade intrínseca á actividade podemos variala en función do alumnado: abonda con cambiar uns números por outros ou unhas imaxes por outras.
No relativo á construción da frase temos, de xeito natural, tres niveis de dificultade diferente (ou máis se incluímos máis imaxes):
- Frase que inclúe só un dos obxectos do cartón. Exemplo:
4 + 5 = 9, conseguido!
Tiña 4 vacas e comprei 5, agora teño 9.
- Frase que inclúe dous obxectos do cartón. Exemplo:
4 + 5 = 9, conseguido!
Tiña 4 vacas, trouxéronme 5 no camión e agora teño 9.
- Frase que inclúe tres obxectos do cartón. Exemplo:
4 + 5 = 9, conseguido!
Había 4 vacas no monte, o camión trouxo 5 e agora hai 9.
Xa un nivel elevado consistiría en que o propio alumnado confeccionase máis cartóns e os resolvese. Quizais para a casa? Sabemos que algún o intentaría por si mesmo e outros reclamarían axuda da familia –o que non é necesariamente mala cousa (permítase a suxestión: tamén a familia pode xogar)–. O problema estaría naqueles que non contasen con axuda e si a necesitasen. É unha cuestión que cómpre analizar en cada caso concreto.
Con medios tecnolóxicos
De dispoñermos de soporte informático, a actividade podería realizarse co ordenador.
Se, por exemplo, temos 19 nenos/as, teríamos un arquivo con 19 cartóns numerados, cada un na súa respectiva páxina.
i) O primeiro exercicio de competencia dixital do alumno sería situarse na páxina que o mestre ou mestra lle indica.
ii) Logo tería que marcar, cambiando de cor, por exemplo, os números que van saíndo (vermellos no exemplo).
iii) E tamén, aínda que noutra cor, os que consiga obter (verde no exemplo).

iv) Escribir as operacións e as frases nos recadros correspondentes.
v) Cando se remate a actividade, cadaquén debe gravar os trocos na súa carpeta, que previamente se crearía dentro da sesión do mestre ou mestra. Isto supón, para nós, contar cos traballos e poder revisalos.
Procesos xerais e específicos da matemática inmersos
A toma de decisións é consubstancial á resolución de problemas, actividade matemática por excelencia.
Neste xogo, en cada chanzo, quen resolve ten que elixir os datos entre os dispoñibles e a operación conveniente que o conduza ao resultado desexado.
Realizándoo con frecuencia enfrontará situacións semellantes, pero dispondo doutros datos. Por exemplo, 6 – 4 = 2, ou 6 – 2 = 4, ou 2 + 4 = 6... fará tomar conciencia das posibilidades de combinar os mesmos números de diferentes xeitos, con tal de adaptar a función que realizan (sumar ou restar, neste exemplo; multiplicar ou dividir, noutros que vemos deseguido).
Iso é, exactamente, a base conceptual da resolución de ecuacións que posteriormente encontrarán (posiblemente en 2.º ou 3.º da ESO) cando estuden as bases da álxebra.
Estimúlase o cálculo mental e a memorización das táboas (primeiro da suma e logo da multiplicación), requisito este sen o cal a andaina polas rutas da matemática sería pesada e lenta.
Tampouco nos deixa dúbida da contribución que se fai ao desenvolvemento da competencia en autonomía e iniciativa persoal, inherente ao propio xogo.
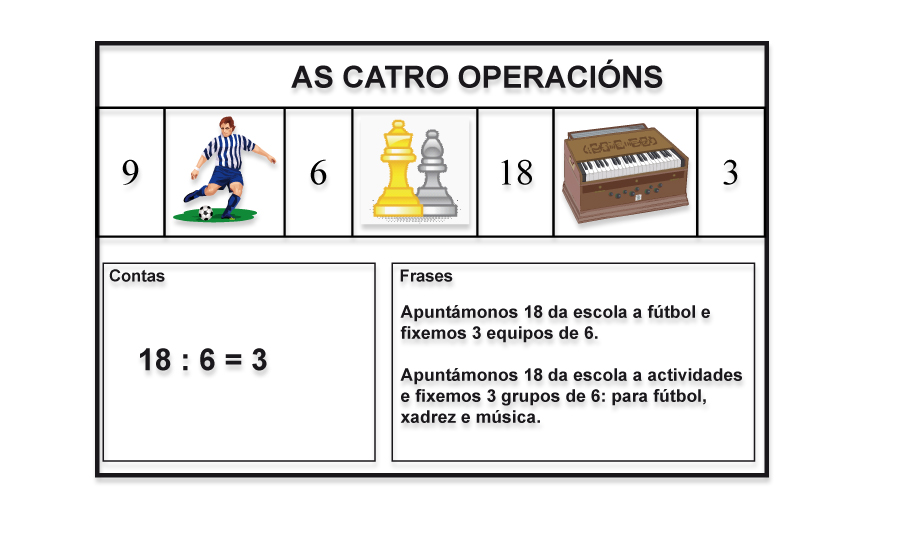
Exemplo para o segundo ciclo
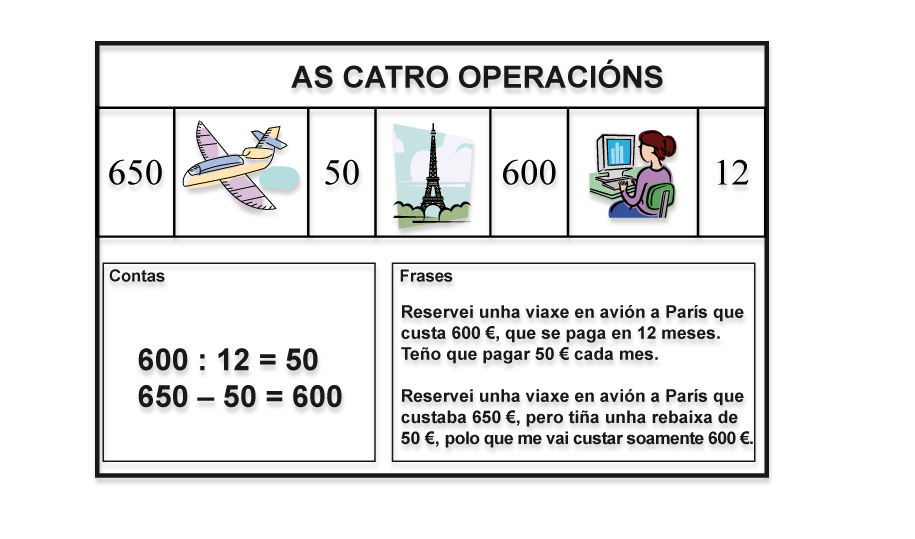
 Exemplo para o terceiro ciclo
Exemplo para o terceiro ciclo
- BACHELARD, G. (1975): "La formation de l'esprit scientifique. París, De Vrin". Versión castelá (1985) La formación del espíritu científico. México, Siglo XXI.
- BRUNER, J. (1956): A study of thinking. Nova York, Wiley. Tradución ao castelán (1978): El proceso mental en el aprendizaje. Madrid, Narcea.
- CHEVALLARD, Y.; BOSCH, M. e GASCÓN, J. (1997): Estudiar Matemáticas: el eslabón perdido entre enseñanza y aprendizaje. Barcelona, ICE-Horsori Editorial.
- COCKROFT et al. (1985): Las Matemáticas si cuentan. Madrid, MECD.
- D´AMORE, B. (2006): Didáctica de la matemática. Bogotá, Ed. Magisterio.
- ENTWISTLE, N. (1988): La comprensión del aprendizaje en el aula. Barcelona, Paidós/MEC.
- FREUDENTHAL, H. (1983): Didactical phenomenology of Mathematical Structures. Dordrecht-Holland, D. Reidel Publishing Company.
- IBARROLA, B. (2009): Crecer con emoción. El desarrollo de la competencia emocional en educación infantil. SM Ed.
- MAYER, R. E. (1986): Pensamiento, resolución de problemas y cognición. Barcelona, Paidós.
- NICKERSON, R.; PERKINS, D. e SMITH, E. (1990): Enseñar a pensar. Barcelona, Paidós/MEC.
- PIAGET, J. (1950): Introduction á l´épistémologie genétique. Presse Universitaries de France. Tradución ao castelán (1987): Introducción a la epistemología genética. México, Paidós.
- PÓLYA, G. (1945): How to solve it. Princeton University Press. Tradución ao castelán (1986): Cómo plantear y resolver problemas. México, Trillas.
- POLYA, G. (1994): "Métodos matemáticos en la ciencia". La tortuga de Aquiles, 3. Madrid, Euler.
- RESNICK, B. e FORD, W. (1991): La enseñanza de las matemáticas y sus fundamentos psicológicos. Barcelona, Paidós/MEC.
- SARRAMONA, J. (2004): Las competencias básicas en la educación obligatoria. Barcelona, Ediciones Ceac.
- SCHOENFELD, A.H. (1987): "What's all the fuss about metacognition?". En A. H. Schoenfeld (ed.): Cognitive science and mathematical education. Philadelphia, Lawrence Erlbaum.
- SHAYER, M. e ADEY, R. (1986): La ciencia de enseñar ciencia. Madrid, Narcea Ediciones.





















